给定二叉树的前序、中序、后续遍历其中两种,如何构造二叉树?
1. 给定前序、中序遍历
In-order: F, B, A, E, H, C, D, I, G
Pre-order: H, B, F, E, A, C, D, G, I
由于前序遍历最先访问根节点。可以确定H为根节点。而中序遍历的顺序为:左子树、根、右子树。所以可以确定中序遍历中,H前面的所有元素构成左子树。后面的所有元素构成右子树。由此可以做如下划分:
In-order: F, B, A, E, H, C, D, I, G
Pre-order: H, B, F, E, A, C, D, G, I
其中红色为根节点、蓝色为左子树、绿色为右子树。
然后递归的对左子树和右子树做同样的操作。最终构建的二叉树为:
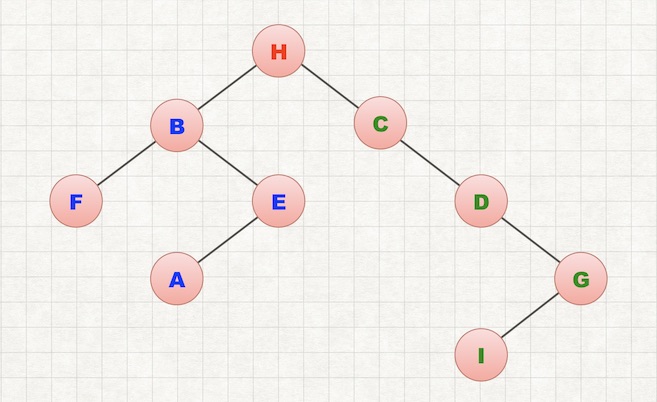
同理,给定其他遍历顺序时,颜色划分如下。
2. 给定后序、中序遍历
In-order: F, B, A, E, H, C, D, I, G
Post-order: F, A, E, B, I, G, D, C, H
3. 给定前序、后序遍历
Pre-order: H, B, F, E, A, C, D, G, I
Post-order: F, A, E, B, I, G, D, C, H
这种情况下,我们首先能判断根节点是H,接下来是如何判断左右子树。
由于后序遍历最后访问根节点。所以根节点之前的所有元素,构成了以该点为根的子树。通过先序遍历,我们知道B是左子树的根节点。在后序遍历中找到B,那么B前面的所有节点即为左子树。因此我们就找到了左右子树。如下:
Pre-order: H, B, F, E, A, C, D, G, I
Post-order: F, A, E, B, I, G, D, C, H
对左右子树进行同样的操作,即可得到整个树。
后记:
遇到给定二叉树的两种遍历序列后,求第三种遍历序列都可以用上述的方法,先构建出树。再给出另外一种遍历序列。



